Introduction

AI is the new hot thing, there’s an abundance of models that are being released frequently. These models have shown impressive capabilities in a wide range of tasks and if you are a researcher or a practitioner, you’ve probably used one of these models in your work. Maybe you’d like to finetune one of them on a particular task, but you don’t have GPUs big enough to do so. If that is the case, fear not, LoRA is here to help you.

What is LoRA?

Finetuning a model usually involves updating all the model’s weights, which is costly and time-consuming. Suppose that you’ve managed to finetune a model on a particular task but it costed you a lot of time and ressources. Now you’d like to finetune the model on a different task, you’d have to repeat the same process with the same cost or even more and unfortunately, not everyone is GPU rich.

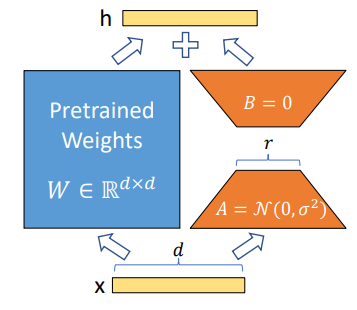
LoRA stands for “Low-Rank Adaptation”, it’s a reparametrization-based finetuning method proposed by Hu et al. in 2021. LoRA proposes an interesting approach to speed up finetuning while preserving the model’s performance. The intuition behind LoRA is that the model’s weights matrix $W_0$ can be represented as the decomposition of a low-rank matrix $W_0 + \Delta W = W_0 + BA$. Nonetheless, it is important to note that $W_0$ is not modified during training, only $\Delta W$ values are updated. But before diving into the details, let’s have a quick reminder about matrix rank.

A quick reminder about matrix rank

The rank $r$ of a matrix is the number of linearly independent row or column vectors in a matrix. In other words, it’s the number of row or column vectors that are not a linear combination of other vectors. For example, the rank of the following matrix is $2$.

$$\begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9 \end{bmatrix}$$

The vector $c_1 = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix}$ is a linear combination of $c_2 = \begin{bmatrix} 2 & 4 & 6 \end{bmatrix}$. Indeed, $c_1 = 2 c_2$ and there no such $\lambda$ that satisfies the equation $c_2 = \lambda c_3$.

LoRA in action

As stated before, given our original weights matrix $W_0 \in \mathbb{R}^{d \times k}$, it can be represented as the sum of two matrices $W_0 + \Delta W = W_0 + BA$. The $\Delta W$ matrix can be decomposed into two matrices $B \in \mathbb{R}^{d \times r}$ and $A \in \mathbb{R}^{r \times k}$, where the rank $r \ll min(d,k)$. During training $W_0$ is frozen. Both $W_0$ and $\Delta W$ are multiplied with the same input $x$ and the product $\Delta Wx$ is scaled by a factor $\frac{\alpha}{r}$, where $\alpha$ is a multiple of $r$. The output of the model is the sum of the two outputs:

$$h = W_0x + \Delta Wx = W_0x + BAx$$

$A$ is initialized using a random Gaussian $\mathcal{N}(0, \sigma^2)$ distribution and $B$ with zeros. These two matrices ($A$ and $B$) are small enough to allow you to finetune your model on many different tasks and deploy it while remaining compute and storage efficient. So if you’d like to use the model on task on which it has already been finetuned, just swap the matrices and you’re good to go.

How to use LoRA?

If you are familiar with 🤗HuggingFace ecosystem then you’ve probably heard about PEFT . PEFT stands for “Parameter Efficient Fine-Tuning”, it’s a library that allows you to finetune your model using LoRA or other adaptation methods. The usage is pretty straightforward. To use it you can proceed as follows for example:

from transformers import AutoModelForCausalLM
from peft import get_peft_model, LoraConfig, TaskType

model = AutoModelForCausalLM.from_pretrained("model_name")
config = LoraConfig(
    r=8, # the rank r is a hyperparameter
    inference_mode=False,
    lora_alpha=32,
    lora_dropout=0.1,
    task_type=TaskType.CAUSAL_LM,
    target_modules=[...] # list of modules to apply LoRA to
    ... # other parameters
)

peft_model = get_peft_model(model, config)

And that’s it, you can now use peft_model as you would use model. You can train it as you wish, whether it’s with transformers Trainer or your own training loop.

Do note that currently, only torch.nn.Linear, torch.nn.Embedding, torch.nn.Conv2d, transformers.pytorch_utils.Conv1D are supported. For a custom module, you can use PyTorch’s parametrization utilities .

Bonus tip

You may also consider using quantization and model compilation with torch.compile to speed up your model.

Conclusion

LoRA is an efficient method to finetune a model while preserving its performance. By leveraging great tools from the ML community, you can easily have a solution tailored to your needs while being GPU poor.